Question

A cylindrical tank of methanol has a mass of 70 kg and a volume of 75 L. Determine the methanol’s weight, density, and specific gravity. Take the gravitational acceleration to be 9.81 m/s2. Also, estimate how much force is needed to accelerate this tank linearly at 0.25 m/s2. The density of water is 1000 kg/m3.

Answer 1

Weight=686.7N,
`\rho=933kg/m^(3)`, S.G.=0.933, F=17.5N

Step-by-step explanation:

So, the first value the problem is asking us for is the weight of methanol. (This is supposing there is a mass of methanol of 70kg inside the tank). We can find this by using the formula:

W=mg

so we can substitute the data the problem provided us with to get:

`W=70kg(9.81m/s^(2))`

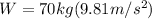
which yields:

W=686.7N

Next, we need to find the density of methanol, which can be found by using the following formula:

`\rho=(m)/(V)`

we know the volume of methanol is 75L, so we can convert that to
`m^(3)` like this:

`75L*(0.001m^(3))/(1L)=0.075m^(3)`

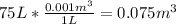
so we can now use the density formula to find our the methanol's density, so we get:

`\rho=(m)/(V)`

`\rho=(70kg)/(0.075m^(3))`

`\rho=933.33kg/m^(3)`

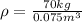
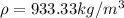
Next, we can us these values to find the specific gravity of methanol by using the formula:

`S.G.=\frac{\rho_(sample)}{\rho_{H_(2)O}}`

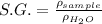
when substituting the known values we get:

`S.G.=(933.33kg/m^(3))/(1000kg/m^(3))`

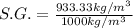
so:

S.G.=0.933

We can now find the force it takes to accelerate this tank linearly at
`0.25m/s^(2)`

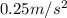
F=ma

`F=(70kg)(0.25m/s^(2))`

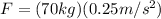
F=17.5N