(a)
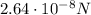 north
north
We can treat the aircraft as a single point charge moving in a magnetic field. In this case, the magnetic force exerted on the plane is
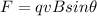
where
 is the charge on the plane
is the charge on the plane
v = 660 m/s is the velocity
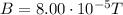 is the magnitude of the magnetic field
is the magnitude of the magnetic field
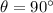 is the angle between the direction of motion of the jet and of the magnetic field
is the angle between the direction of motion of the jet and of the magnetic field
Substituting,

The direction can be found by using Fleming's left hand rule. We have:
- index finger: magnetic field direction (straight up)
- middle finger: velocity of the plane (due west)
- force: thumb --> north
(b) Not negligible
As we can see from part (a), the magnitude of the force is not really big, so the effects are negligible.
For instance, we can compare this force with the weight of a plane. If we take a Boeing 737, its mass is about 80,000 kg, so its weight is
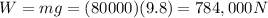
As we can see, this is several orders of magnitude bigger than the magnetic force calculated at point (a), so the effects of the magnetic force are negligible.