Answer:
86 mm
Step-by-step explanation:
From the attached thermal circuit diagram, equation for i-nodes will be
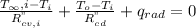 Equation 1
Equation 1
Similarly, the equation for outer node “o” will be
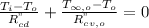 Equation 2
Equation 2
The conventive thermal resistance in i-node will be
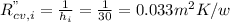 Equation 3
Equation 3
The conventive hermal resistance per unit area is
 Equation 4
Equation 4
The conductive thermal resistance per unit area is
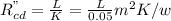 Equation 5
Equation 5
Since
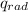 is given as 100,
is given as 100,
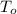 is 40
is 40
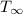 is 300
is 300
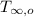 is 25
is 25
Substituting the values in equations 3,4 and 5 into equations 1 and 2 we obtain
 Equation 6
Equation 6
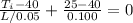

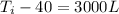
 Equation 7
Equation 7
From equation 6 we can substitute wherever there’s
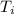 with 3000L+40 as seen in equation 7 hence we obtain
with 3000L+40 as seen in equation 7 hence we obtain
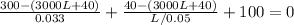
The above can be simplified to be
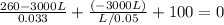
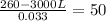
-3000L=1.665-260
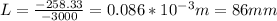
Therefore, insulation thickness is 86mm