Answer:
1- A critical value right-tailed Normality test.
2- Yes, they did.
3-
Null hypothesis
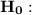 The national average on the statistics achievement test is 60
The national average on the statistics achievement test is 60
Alternative hypothesis
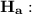 The average on the experimental program for statistics education is greater than 60
The average on the experimental program for statistics education is greater than 60
4- 0.05 or 5%
5- A Type 1 Error is the error we make when we reject the null hypothesis given that it is true.
Explanation:
1)
Since the sample size is greater than 30, the population follows a Normal distribution, and we suspect the average is greater than the established one, the appropriate test to use is a critical value right-tailed Normality test.
2)
To check if the students scored significantly above the national average in this special program to a significance level α = 0.05, we must check if the z-statistic given by the sample falls to the right of 1.64, since the area under the Normal N(0;1) to the right of 1.64 equals 0.05
Our z-statistic is given by the formula
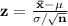
where
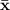 is the mean of the sample
is the mean of the sample
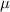 is the mean of the null hypothesis
is the mean of the null hypothesis
 is the standard deviation
is the standard deviation
n is the sample size
Our z-statistic is then
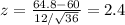
Since 2.4 > 1.64, the students did score significantly above the national average in this special program to a significance level α = 0.05
3)
Null hypothesis
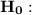 The national average on the statistics achievement test is 60
The national average on the statistics achievement test is 60
Alternative hypothesis
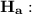 The average on the experimental program for statistics education is greater than 60
The average on the experimental program for statistics education is greater than 60
4)
The probability of a Type 1 Error is 0.05 or 5% (the significance level)
5)
A Type 1 Error is the error we make when we reject the null hypothesis given that it is true.