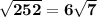Answer:
1)
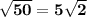
2)
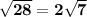
3)
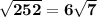
Explanation:
We need to simplify the radicals:
1)
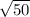
First we find prime factors of 50
50 = 2 x 5 x 5
Now,
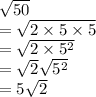
So,
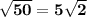
2)
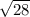
First we find prime factors of 28
28 = 2 x 2 x 7
Now,
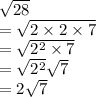
So,
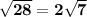
3)
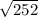
First we find prime factors of 252
50 = 2 x 2 x 3 x 3 x 7
Now,
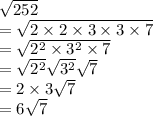
So,