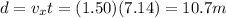1) 26.6 m
Along the horizontal direction, the lunch pail is moving with a uniform motion (constant speed), since there are no forces acting in this direction.
Therefore, the distance travelled horizontally after a time t is given by:
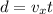
where we know
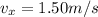 is the horizontal velocity
is the horizontal velocity
d = 3.50 m is the distance covered horizontally
Solving for t, we find the total time of the motion:
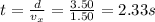
Now we know that the pail takes 2.33 s to fall to the ground. We can now consider the vertical motion of the pail, which is a free fall motion, so the vertical displacement is given by the equation

where, taking downward as positive direction:
u = 0 is the initial vertical velocity
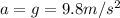 is the acceleration of gravity
is the acceleration of gravity
Substutting t = 2.33 s, we find how fat the pail has fallen:
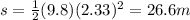
2) 10.7 m
In this case, we know instead the vertical displacement:

Therefore, we can use the same equation again

To find the total time of motion:

We know that along the horizontal direction, the velocity is constant:
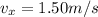
So, the horizontal distance covered in this time is