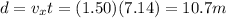Question

A lunch pail is accidentally kicked off a steel beam on a building under construction. Suppose the initial horizontal speed is 1.50 m/s. How far does the lunch pail fall after it travels 3.50 m horizontally? 8. If the building in problem 7 is 2.50 × 10 2 m tall, and the lunch pail is knocked off the top floor, what will be the horizontal displacement of the lunch pail when it reaches the ground?

Answer 1

1) 26.6 m

Along the horizontal direction, the lunch pail is moving with a uniform motion (constant speed), since there are no forces acting in this direction.

Therefore, the distance travelled horizontally after a time t is given by:

`d=v_x t`

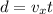
where we know

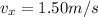`v_x = 1.50 m/s` is the horizontal velocity

d = 3.50 m is the distance covered horizontally

Solving for t, we find the total time of the motion:

`t=(d)/(v_x)=(3.50)/(1.50)=2.33 s`

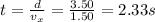
Now we know that the pail takes 2.33 s to fall to the ground. We can now consider the vertical motion of the pail, which is a free fall motion, so the vertical displacement is given by the equation

`s=ut+(1)/(2)at^2`

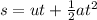
where, taking downward as positive direction:

u = 0 is the initial vertical velocity

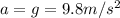`a=g=9.8 m/s^2` is the acceleration of gravity

Substutting t = 2.33 s, we find how fat the pail has fallen:

`s=(1)/(2)(9.8)(2.33)^2=26.6 m`

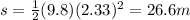
2) 10.7 m

In this case, we know instead the vertical displacement:

`s=2.50\cdot 10^2 m = 250 m`

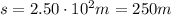
Therefore, we can use the same equation again

`s=ut+(1)/(2)at^2`

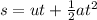
To find the total time of motion:

`t=\sqrt{(2s)/(a)}=\sqrt{(2(250))/(9.8)}=7.14 s`

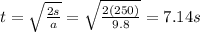
We know that along the horizontal direction, the velocity is constant:

`v_x = 1.50 m/s`

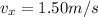
So, the horizontal distance covered in this time is

`d=v_x t = (1.50)(7.14)=10.7 m`