Question

Two electrons travel towards each other at 0.2 c parallel to the laboratory x-axis. What is the relative velocity of one electron with respect to the other? What is the relative velocity of the two electrons with respect to the lab?

Answer 1

1) In the reference frame of one electron: 0.38c

To find the relative velocity of one electron with respect to the other, we must use the following formula:

`u'=(u-v)/(1-(uv)/(c^2))`

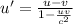
where

u is the velocity of one electron

v is the velocity of the second electron

c is the speed of light

In this problem:

u = 0.2c

v = -0.2c (since the second electron is moving towards the first one, so in the opposite direction)

Substituting, we find:

`u'=(0.2c+0.2c)/(1+((0.2c)(0.2c))/(c^2))=(0.4c)/(1+0.04)=0.38c`

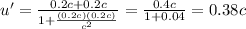
2) In the reference frame of the laboratory: -0.2c and +0.2c

In this case, there is no calculation to be done. In fact, we are already given the speed of the two electrons; we are also told that they travel in opposite direction, so their velocities are

+0.2c

-0.2c