Answer:
The correct graph is D.
Explanation:
Given a quadratic equation :
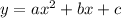
You can find the roots (where the graph intersects the x-axis) applying the following equation :
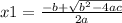
and

We define the discriminant as
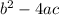
If
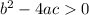 then the graph will intersect the x-axis in two points
then the graph will intersect the x-axis in two points
If
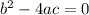 then the graph will intersect the x-axis in one point.
then the graph will intersect the x-axis in one point.
Finally, If
 then the graph won't intersect the x-axis because it will not have real roots.
then the graph won't intersect the x-axis because it will not have real roots.
In this exercise, the graph that doesn't intersect the x-axis is graph D.