Question

Which is the graph of a quadratic equation that has a negative discriminant?

Answer 1

D

Explanation:

A negative discriminant indicates that the quadratic equation has no real roots.

Thus the graph does not touch or intersect the x- axis

The only graph that does not touch or intersect the x- axis is the fourth one

Answer 2

The correct graph is D.

Explanation:

Given a quadratic equation :

`y=ax^(2)+bx+c`

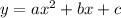
You can find the roots (where the graph intersects the x-axis) applying the following equation :

`x1=\frac{-b+\sqrt{b^(2)-4ac}}{2a}`

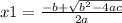
and

`x2=\frac{-b-\sqrt{b^(2)-4ac}}{2a}`

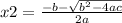
We define the discriminant as
`b^(2)-4ac`

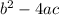
If
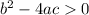`b^(2)-4ac>0` then the graph will intersect the x-axis in two points

If
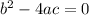`b^(2)-4ac=0` then the graph will intersect the x-axis in one point.

Finally, If
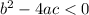`b^(2)-4ac<0` then the graph won't intersect the x-axis because it will not have real roots.

In this exercise, the graph that doesn't intersect the x-axis is graph D.