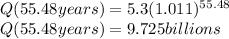Question

The world population at the beginning of 1990 was 5.3 billion. Assume that the population continues to grow at the rate of approximately 2%/year and find the function Q(t) that expresses the world population (in billions) as a function of time t (in years), with t = 0 corresponding to the beginning of 1990.(a) If the world population continues to grow at approximately 2%/year, find the length of time t0 required for the population to triple in size.

t0 = 1 yr
(b) Using the time t0 found in part (a), what would be the world population if the growth rate were reduced to 1.1%/yr?

Answer 1

a). 55.47 years

b). population = 9.72 billion

Explanation:

Since population growth is an exponential phenomenon, population after t years will be represented by,

`P_(t)=P_(0)(1+0.02)^(t)`

[Since rate of population growth is 2%]

`P_(t)=P_(0)(1.02)^(t)`

Where
`P_(t)` = Population after t years

`P_(0)` = Population at t = 0 years

A). Now we have to find the time by which the population will triple in size.

Therefore, for
`P_(t)=3P_(0)`

`3P_(0)=P_(0)(1.02)^(t)`

`3=(1.02)^(t)`

By taking log on both the sides of the equation.

`log3=log(1.02)^(t)`

0.4771212 = tlog(1.02)

0.4771212 = t(0.0086)

t =
`(0.4771212)/(0.0086)`

= 55.47 years

B). If growth rate was reduced to 1.1% per year then we have to find the world population after t = 55.47 years and
`P_(0)` = 5.3 billion

`P_(t)=5.3(1+0.011)^(55.47)`

`P_(55.47)=5.3(1.011)^(55.47)`

= 5.3×1.8346

= 9.72 billion

Answer 2

a)55.48 years

b)9.725 billions

Explanation:

First of all, note that when you increase certain amount by x percent, you only have to multiply that amount for a decimal number following this rule:

`New=Original(1+(x)/(100))`

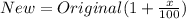
For example, if you increase 5.3 billion by 20%, then:

`New=5.3billion(1+(20)/(100))\\ New=5.3billion(1.2)`

`New=6.36 billion`

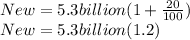
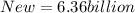
In the problem you need to increase the population by 2%/year, then after one year you'll have:

`Q=5.3(1+(2)/(100))billions\\Q=5.3(1.02) billions\\Q=5.406 billions`

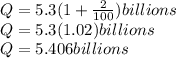
Note that this last quantity will increase 2% in the second year, then:

`Q(2)=5.3(1.02)(1.02) billions\\Q(2)=5.3(1.02)^(2) billions`

In the third year the population will be:

`Q(3)=5.3 (1.02)(1.02)(1.02)\\Q(3)=5.3(1.02)^(3) billions`

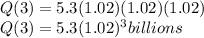
Then, the function Q(t) that expresses the world population (in billions) is given by:

`Q(t)=5.3 (1.02)^(t)`

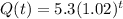
where t=0 corresponds to the beginning of 1990 (5.3 billions).

a)The time necessary for the population to triple in size is given by:

`3(5.3)=5.3(1.02)^(t)\\ 3=1.02^(t)`

To solve for t, you need to apply the natural logarithm or the common logarithm in both sides of the equation:

`ln(3)=ln[(1.02)^(t)]\\ln(3)=t(ln(1.02))\\t=(ln(3))/(ln(1.02))\\ t=55.48 years`

Then, the time required to the population to triple in size is 55.48 years.

b)If the growth rate were reduced to 1.1%/year, the function would be:

`Q(t)=5.3(1+(1.1)/(100) )^(t)\\Q(t)=5.3(1.011)^(t)`

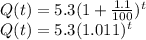
The world population at the time obtained in a) would be:

`Q(55.48years)=5.3(1.011)^(55.48)\\ Q(55.48years)=9.725 billions`