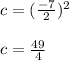Question

What value for c will make the expression a perfect square trinomial? x2 – 7x + c negative StartFraction 49 Over 4 EndFraction negative seven-halves seven-halves StartFraction 49 Over 4 EndFraction

Answer 1

49|4

Explanation:

Answer 2

Answer:
`c=(49)/(4)`

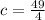
Explanation:

You can find the value of "c" that will make it a perfect square trinomial by Completing the square.

Given the following expression provided in the exercise:

`x^2 - 7x + c`

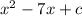
You can notice that it is written in this form:

`ax^2-bx+c`

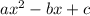
Then, you can identify that the coefficient "b" is:

`b=-7`

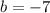
Since to complete the square you must add and subtract the half of square of coefficient "b", you can conclude that:

`c=((b)/(2))^2`

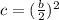
Therefore, substituting "b" into
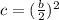`c=((b)/(2))^2`, you get:

`c=((-7)/(2))^2\\\\c=(49)/(4)`