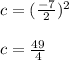Answer:
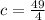
Explanation:
You can find the value of "c" that will make it a perfect square trinomial by Completing the square.
Given the following expression provided in the exercise:
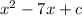
You can notice that it is written in this form:
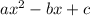
Then, you can identify that the coefficient "b" is:
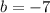
Since to complete the square you must add and subtract the half of square of coefficient "b", you can conclude that:
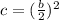
Therefore, substituting "b" into
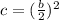 , you get:
, you get: