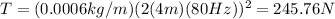Answer:
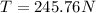
Step-by-step explanation:
We know that the frequency of the nth harmonic is given by
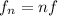 , where
, where
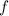 is the fundamental harmonic. Since we have the values of two consecutive frequencies, we can do:
is the fundamental harmonic. Since we have the values of two consecutive frequencies, we can do:
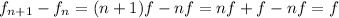
Which for our values means (we do not need the value of n, that is, which harmonics are the frequencies given):
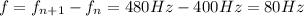
Now we turn to the formula for the vibration frequency of a string (for the fundamental harmonic):
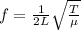
So the tension is:
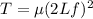
Which for our values is: