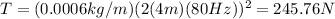Question

A string with a length of 4.00 m is held under a constant tension. The string has a linear mass density of \mu=0.000600~\text{kg/m}μ=0.000600 kg/m. Two resonant frequencies of the string are 400 Hz and 480 Hz. There are no resonant frequencies between the two frequencies. What is the tension in the string?

Answer 1

`T=245.76N`

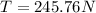
Step-by-step explanation:

We know that the frequency of the nth harmonic is given by
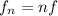`f_n=nf`, where
`f` is the fundamental harmonic. Since we have the values of two consecutive frequencies, we can do:

`f_(n+1)-f_n=(n+1)f-nf=nf+f-nf=f`

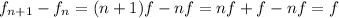
Which for our values means (we do not need the value of n, that is, which harmonics are the frequencies given):

`f=f_(n+1)-f_n=480Hz-400Hz=80Hz`

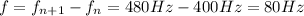
Now we turn to the formula for the vibration frequency of a string (for the fundamental harmonic):

`f=(1)/(2L) \sqrt{(T)/(\mu)}`

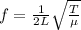
So the tension is:

`T=\mu(2Lf)^2`

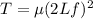
Which for our values is:

`T=(0.0006kg/m)(2(4m)(80Hz))^2=245.76N`