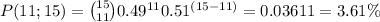Answer:
3.61%
Explanation:
This situation can be modeled with the Binomial Distribution which computes the likelihood of an event “success” that occurs exactly k times out of n, and is given by
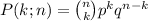
where
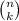 = combination of n elements taken k at a time.
= combination of n elements taken k at a time.
p = probability that the event (“success”) occurs once
q = 1-p
In this case, we define “success” as a college student not being confident that their major would lead to a good job.
Then
p = 49% = 0.49
q = 51% = 0.51
“If 15 college students are chosen at random, what's the probability that 11 of them are NOT confident that their major would lead to a good job?”
Here we are looking for P(11;15)