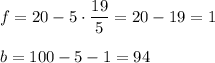Answer:
5 cats, 1 fish and 94 birds
Explanation:
Let
- c be the number of cats;
- b be the number of birds;
- f be the number of fish.
A kid bought 100 toy animals, then
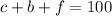
If a cat costs $10.00, then c cats cost $10c.
If a fish costs $3.00, then f fish cost $3f.
If a bird costs $0.50, then b birds cost $0.5b.
In total,
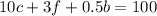
We get the system of two equations:
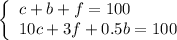
From the first equation:
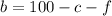
Substitute it into the second equation:
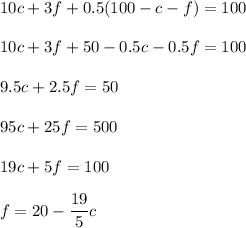
Number f must be a whole number greater than 0, so
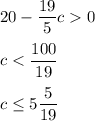
Number c must be a multiple of 5, thus the only possible value for c is 5.
When c = 5, then