Question

A kid spent $100.00 to get 100 toy animals. The child bought at least one cat, one fish, and one bird, and did not buy any other toy animals. If a cat costs $10.00, a fish costs $3.00, and a bird costs $0.50, how many of each toy did the child buy?

Answer 1

5 cats, 1 fish and 94 birds

Explanation:

Let

• c be the number of cats;
• b be the number of birds;
• f be the number of fish.

A kid bought 100 toy animals, then

`c+b+f=100`

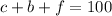
If a cat costs $10.00, then c cats cost $10c.

If a fish costs $3.00, then f fish cost $3f.

If a bird costs $0.50, then b birds cost $0.5b.

In total,

`10c+3f+0.5b=100`

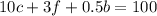
We get the system of two equations:

`\left\{\begin{array}{l}c+b+f=100\\10c+3f+0.5b=100\end{array}\right.`

From the first equation:

`b=100-c-f`

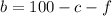
Substitute it into the second equation:

`10c+3f+0.5(100-c-f)=100\\ \\10c+3f+50-0.5c-0.5f=100\\ \\9.5c+2.5f=50\\ \\95c+25f=500\\ \\19c+5f=100\\ \\f=20-(19)/(5)c`

Number f must be a whole number greater than 0, so

`20-(19)/(5)c>0\\ \\c<(100)/(19)\\ \\c\le 5(5)/(19)`

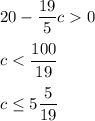
Number c must be a multiple of 5, thus the only possible value for c is 5.

When c = 5, then

`f=20-5\cdot (19)/(5)=20-19=1\\ \\b=100-5-1=94`