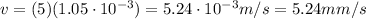Question

(a) Write an equation describing a sinusoidal transverse wave traveling on a cord in the positive of a y axis with an angular wave number of a period of 0.20 s, and an amplitude of 3.0 mm. Take the transverse direction to be the z direction.

(b) What is the maximum transverse speed of a point on the cord?
(c) What is the wave speed?

Answer 1

Missing data: the wave number

`k=60 cm^(-1)`

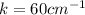
(a)
`z = 0.003 sin (6000y-31.4 t)`

For a transverse wave travelling in the positive y-direction and with vibration along the z-direction, the equation of the wave is

`z = A sin (ky-\omega t)`

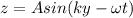
where

A is the amplitude of the wave

k is the wave number

`\omega` is the angular frequency

t is the time

In this situation:

A = 3.0 mm = 0.003 m is the amplitude

`k = 60 cm^(-1) = 6000 m^(-1)` is the wave number

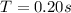`T = 0.20 s` is the period, so the angular frequency is

`\omega=(2\pi)/(T)=(2\pi)/(0.20)=31.4 rad/s`

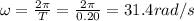
So, the wave equation (in meters) is

`z = 0.003 sin (6000y-31.4 t)`

(b) 0.094 m/s

For a transverse wave, the transverse speed is equal to the derivative of the displacement of the wave, so in this case:

`v_t = z' = -A \omega cos (ky-\omega t)`

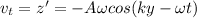
So the maximum transverse wave occurs when the cosine term is equal to 1, therefore the maximum transverse speed must be

`v_(t)_(max) =\omega A`

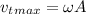
where

`\omega = 31.4 rad/s\\A = 0.003 m`

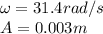
Substituting,

`v_(t)_(max)=(31.4)(0.003)=0.094 m/s`

(c) 5.24 mm/s

The wave speed is given by

`v=f \lambda`

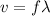
where

f is the frequency of the wave

`\lambda` is the wavelength

The frequency can be found from the angular frequency:

`f=(\omega)/(2\pi)=(31.4)/(2\pi)=5 Hz`

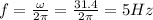
While the wavelength can be found from the wave number:

`\lambda = (2\pi)/(k)=(2\pi)/(6000)=1.05\cdot 10^(-3) m`

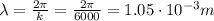
Therefore, the wave speed is

`v=(5)(1.05\cdot 10^(-3) )=5.24 \cdot 10^(-3) m/s = 5.24 mm/s`