Question

15.

(a) An oxygen‐16 ion with a mass of 2.66 10 kg 26  travels at 5.00 10 m/s 6  perpendicular to a 1.20‐T magnetic field, which makes it move in a circular arc with a 0.231‐m radius. What positive charge is on the ion?
(b) What is the ratio of this charge to the charge of an electron?
(c) Discuss why the ratio found in (b) should be an integer.

Answer 1

(a)
`4.8\cdot 10^(-19) C`

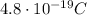
The radius of the trajectory of a charged particle moving perpendicular to a magnetic field is given by

`r=(mv)/(qB)`

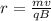
where

m is the mass of the particle

q is its charge

v is its velocity

B is the strength of the magnetic field

In this problem, we have:

`m=2.66\cdot 10^(-26) kg`

`v=5.00\cdot 10^6 m/s`

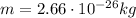
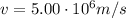
B = 1.20 T

r = 0.231 m

Solving for q, we find its charge:

`q=(mv)/(rB)=((2.66\cdot 10^(-26))(5.00\cdot 10^6))/((0.231)(1.20))=4.8\cdot 10^(-19) C`

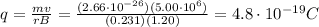
(b) 3

The charge of an electron is

`e=1.6\cdot 10^(-19)C`

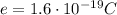
While the charge of this oxygen ion is

`q=4.8\cdot 10^(-19)C`

So, the ratio between the two charges is

`(q)/(e)=(4.8\cdot 10^(-19))/(1.6\cdot 10^(-19))=3`

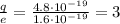
(c) Because an ion is an atom that has gained/lost an integer number of electrons

An ion is an atom that has gained/lost an integer number of electrons. In this particular case, we see that the charge of the oxygen ion is 3 times that of the electron: this means that the ion has gained/lost exactly 3 electrons.

The ratio found in part (b) cannot be a fraction, because that would mean that the atom has gained/lost a fractional number of electrons: but this is impossible, since the electron is a fundamental particle so it cannot be "divided", therefore the ratio must be an integer.