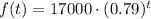We start with a value of 17000 in 2006. For reasons that will soon be clear, let's write it as

One year later, the resale value has decreased by 21%, which implies that the resale value is 79% of the previous one: the resale value in 2007 is
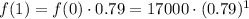
Move again one year forward: the resale price in 2008 is 79% of the resale price in 2007:

So, as you can see, after t years from 2006, the resale value will be multiplied by 0.79 t times, leading to the function