The simplification of (-2 - 2i)( -4 + 6i) is 20 - 4i
SOLUTION:
In this particular question we have been asked to simplify the given equation containing complex numbers.
The given equation is:
(-2-2i)(-4+6i)
To simplify the equation we have to open the brackets and multiply.
Before we do that we need to know the value of i.
‘i’ is as complex number with a value of
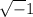 and
and
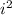 has a value of -1
has a value of -1
So now we can calculate the given expression as follows:
= (-2 - 2i)( -4 + 6i)
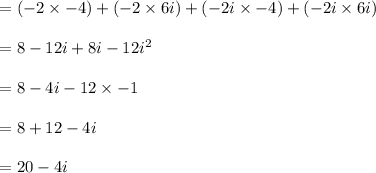
Therefore, the correct option is 20 - 4i.