Given:
A certain function h(x) contains the point (8,-2).
To find:
The value of
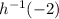 .
.
Solution:
If a function is defined as
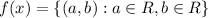
Then, its inverse is defined as
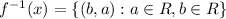
It is given that, a certain function h(x) contains the point (8,-2). It means, its inverse
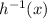 contains the point (-2,8). So, the value of inverse function is 8 at x=-2, i.e.,
contains the point (-2,8). So, the value of inverse function is 8 at x=-2, i.e.,
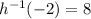
Therefore, the value of
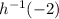 is 8.
is 8.