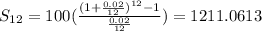Question

117. Sami opens an account and deposits $100 into it at the end of each month. The account earns 2% per year compounded monthly. Let Sn denote the amount of money in her account at the end of n months (just after she makes a deposit). For example, S1 = 100 and S2 = 100(1 + 0.02 /12)+100

c. Find an explicit function for Sn, and use it to find S12.

Answer 1

The explicit function is:

`S_(n) =Pz^(n-1) +C((z^(n-1)-1)/(z-1) )`

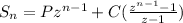
where

`z=(1+(0.02)/(12))`

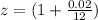
and we calculate S12:

`S_(12) = $1211.06`

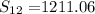
Explanation:

Expanding a few steps of the compound interest:

`S_(1)=100\\S_(2)=S_(1)(1+(0.02)/(12))+100\\S_(3)=S_(2)(1+(0.02)/(12))+100\\...\\S_(n)=S_(n-1)(1+(0.02)/(12))+100`

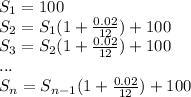
We can write:

`(1+(0.02)/(12))=z`

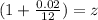
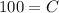`100=C` for deposits

Then, expanding the previous equations would yield:

`S_(1)=C\\S_(2)=Cz + C\\S_(3)=Cz^(2)+Cz + C\\S_(n)=Cz^(n-1) +...+Cz+C`

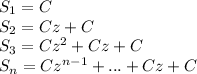
This is a geometric series form, which can be simplified to:

`S_(n)=C((z^(n)-1)/(z-1) )`

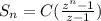
plugin in the values for the 12 month gives:

`S_(12)=100(((1+(0.02)/(12))^(12) -1)/((0.02)/(12)))=1211.0613`