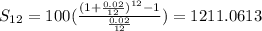Answer:
The explicit function is:
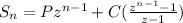
where
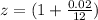
and we calculate S12:
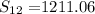
Explanation:
Expanding a few steps of the compound interest:
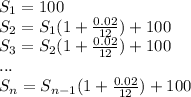
We can write:

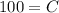 for deposits
for deposits
Then, expanding the previous equations would yield:
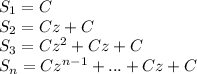
This is a geometric series form, which can be simplified to:
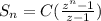
plugin in the values for the 12 month gives: