Answer:
these equations have no solution in the domain of real numbers
Explanation:
Hello! To solve this problem of equations first let's equate equations one and two and perform the procedure to find X
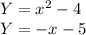
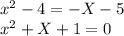
if we solve the quadratic equation we find the following results
![X1=-(1)/(2) +\frac{ \sqrt[2]{3} }{2}i\\X2=-(1)/(2) -\frac{ \sqrt[2]{3} }{2}i](https://img.qammunity.org/2020/formulas/mathematics/high-school/3mzlhakt9zrbl818654o4m6ttnaqpp9gf4.png)
as we can see the two answers result in imaginary numbers which means that the two equations are not intercepted I attached a picture of the graph