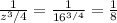Answer:
a) 1/27
b) 16
c) 1/8
Explanation:
a)
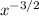
One of the properties of the exponents tells us that when we have a negative exponent we can express it in terms of its positive exponent by turning it into the denominator (and changing its sign), so we would have:
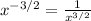
And now, solving for x = 9 we have:
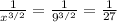
b)
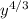
This is already a positive rational exponent so we are just going to substitute the value of y = 8 into the expression
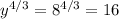
c)
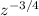
Using the same property we used in a) we have:
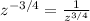
And now, solving for z = 16 we have: