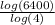Answer:
Explanation:
The initial population of bacteria is 800 and we know that this number is quadrupling every hour.
We're going to find a function in terms of t (time) that gives us the population of bacteria at that time.
Since the population is quadrupling every hour the function in terms of t (where t is expressed in hours) is:
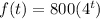
Now we need to find the time when there will be 5,120,000 bacterias. This means the time t when f(t) = 5,120,000
So we have 5,120,000 =
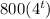
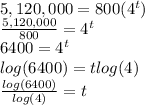
Therefore, the time when there will be 5,120,000 bacterias will be: