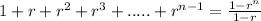Question

70. Suppose that you currently have one credit card with a balance of $10,000 at an annual rate of 24.00% interest. You have stopped adding any additional charges to this card and are determined to pay off the balance. You have worked out the formula bbn = b0r n − R(1 + r+r2 +....+ r n−1), where b0 is the initial balance, bn is the balance after you have maden payments, r= 1 + i, wherei is the monthly interest rate, and R is the amount you are planning to pay each month.

b. Explain why we can rewrite the given formula as bn= b0rn − R(1-rn/1-r).????????

Answer 1

`1+r+r^(2)+r^(3)+.....+r^(n-1) = (1-r^(n))/(1-r)`

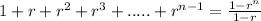
Explanation:

Taking the succession:

`1+r+r^(2)+r^(3)+.....+r^(n-1)`

You can multiply and divide by 1-r without chaging the result:

`(1-r)/(1-r) (1+r+r^(2)+r^(3)+.....+r^(n-1))`

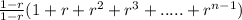
Distributing the upper part of the fraction you have:

`(1)/(1-r) (1-r+r-r^(2)+r^(2)-r^(3)+r^(3)-r^(4)+.....+r^(n-1)-r^(n))`

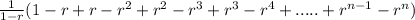
As can be seen all the intermediate members will be canceled by a same member with opposite sign, only
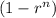`(1-r^(n))` will be left so:

`1+r+r^(2)+r^(3)+.....+r^(n-1) = (1-r^(n))/(1-r)`