Question

A block of copper of unknown mass has an initial temperature of 65.4 degress celcuis. THe copper is immersed in a beaker containing 95.7 g water at 22.7 degress celcius. When the two substances reach thermal equilibrium, the final temperature is 24.2 degrees celcius. What is the mass of the copper block?

Answer 1

The answer to your question is: m = 37.88 g

Step-by-step explanation:

Data

Copper Water

mass ? 95.7 g

Cp 0.092 cal/g°C 1 cal/g°C

T1 65.4°C 22.7°C

T2 24.2°C 24.2°C

Formula

Q copper = Q water

Q = mCp(T2 - T1)

- m(0.092)(24.2 - 65.4) = 95.7(1)(24.2 - 22.7)

m = 95.7(1)(24.2 - 22.7) /- (0.92)(24.2 - 65.4)

m = 143.55 / 3.79

m = 37.88 g

Answer 2

The mass of the copper block is 37.82g

To determine the mass of the copper block, we can use the principle of conservation of energy, specifically the heat transfer equation:

`\[ q_{\text{copper}} = q_{\text{water}} \]`

The heat gained or lost (q) can be calculated using the formula
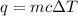`\(q = mc\Delta T\)`, where m is the mass, c is the specific heat capacity, and
`\(\Delta T\)` is the change in temperature.

For copper:

`\[ q_{\text{copper}} = m_{\text{copper}}c_{\text{copper}}\Delta T_{\text{copper}} \]`

For water:

`\[ q_{\text{water}} = m_{\text{water}}c_{\text{water}}\Delta T_{\text{water}} \]`

At thermal equilibrium, the heat gained by the copper is equal to the heat gained by the water:

`\[ m_{\text{copper}}c_{\text{copper}}\Delta T_{\text{copper}} = m_{\text{water}}c_{\text{water}}\Delta T_{\text{water}} \]`

Rearrange the equation to solve for the mass of the copper block
`(\(m_{\text{copper}}\)):`

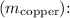
`\[ m_{\text{copper}} = \frac{m_{\text{water}}c_{\text{water}}\Delta T_{\text{water}}}{c_{\text{copper}}\Delta T_{\text{copper}}} \]`

Substitute the given values and solve:

`\[ m_{\text{copper}} = \frac{(95.7 \, \text{g})(4.18 \, \text{J/g}^\circ \text{C})(24.2^\circ \text{C} - 22.7^\circ \text{C})}{(0.385 \, \text{J/g}^\circ \text{C})(65.4^\circ \text{C} - 24.2^\circ \text{C})} \]`

Therefore, The mass of the copper block is 37.82g