Answer:
The function
 is indeed a solution of the two dimensional Laplace equation
is indeed a solution of the two dimensional Laplace equation
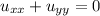 .
.
The wave equation
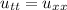 is satisfied by the function
is satisfied by the function
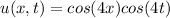 but not by the function
but not by the function
 .
.
Explanation:
To verify that the function
 is a solution of the 2D Laplace equation we calculate the second partial derivative with respect to x and then with respect to t.
is a solution of the 2D Laplace equation we calculate the second partial derivative with respect to x and then with respect to t.

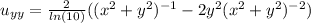
then we introduce it in the equation
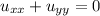
we get that
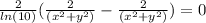
To see if the functions 1)
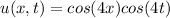 and 2)
and 2)
 solve the wave equation we have to calculate the second partial derivative with respect to x and the with respect to t for each function. Then we see if they are equal.
solve the wave equation we have to calculate the second partial derivative with respect to x and the with respect to t for each function. Then we see if they are equal.
1)
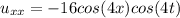
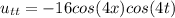
we see for the above expressions that
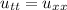
2) with this function we will have to use the chain rule
If we call
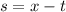 and
and
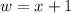 then we have that
then we have that
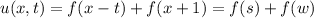
So
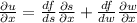
because we have
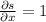 and
and
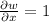
then
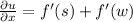
⇒

⇒

⇒
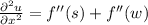
Regarding the derivatives with respect to time
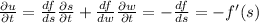
then
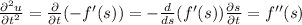
we see that
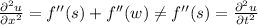
 doesn´t satisfy the wave equation.
doesn´t satisfy the wave equation.