Question

50.The amount of caffeine in a patient’s bloodstream decreases by half every 3.5 hours. A latte contains 150 mg of caffeine, which is absorbed into the bloodstream almost immediately.

b. Do you have enough information to find a model that is appropriate for this situation? Either find a model or
explain what other information you would need to do so.

Answer 1

We have the initial amount of caffeine and the time it takes for it to decrease to half. This is enough information to say that an exponential model is appropriate for this situation.

`C(t) = C(0)e^(-0.197t)`

Explanation:

We have the initial amount of caffeine and the time it takes for it to decrease to half. This is enough information to say that an exponential model is appropriate for this situation.

This situation can be modeled by the following equation:

`C(t) = C(0)e^(rt)`

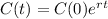
In which
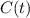`C(t)` is the ammount of caffeine in the blood at time t,
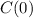`C(0)` is the initial amount and r is the rate that it decreases.

The problem states that

A latte contains 150 mg of caffeine, which is absorbed into the bloodstream almost immediately, so
`C(0) = 150`.

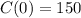The amount of caffeine in a patient’s bloodstream decreases by half every 3.5 hours, so
`C(3.5) = 0.5C(0) = 0.5(150) = 75`.

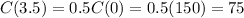With these informations, we can find the value of r in the equation of the model.

`C(t) = C(0)e^(rt)`

`C(3.5) = C(0)e^(3.5r)`

`75 = 150e^(3.5r)`

`e^(3.5r) = 0.5`

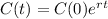
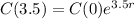
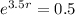
To find the value of r, we can apply ln to both sides of the equation:

`\ln{e^(3.5r)} = ln(0.5)`

`3.5r = -0.69`

`r = -0.197`

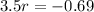
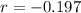
So, the model is:

`C(t) = C(0)e^(-0.197t)`