Question

Use the fact that x⁴+64=(x²-4x+8)(x²+4x+8) to explain how you know that the graph of y=x⁴+64 has no x-intercepts. You need not find the solutions.

Answer 1

The term
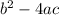`b^(2) - 4ac` for (x²-4x+8) and for (x²+4x+8) is negative.

Explanation:

The x intercepts are the values of x in which the function is equal to zero. So if x⁴+64=(x²-4x+8)(x²+4x+8), the x intercepts are the values of x that satisfy:

(x²-4x+8) = 0 or (x²+4x+8) = 0

Then, the values of x that satisfy (ax²+bx+c) = 0 are calculated as:

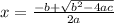`x=\frac{-b+\sqrt{b^(2)-4ac}}{2a}` or

`x=\frac{-b-\sqrt{b^(2)-4ac}}{2a}`

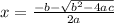
So, if the term
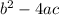`b^(2)-4ac` is negative the graph of the function has no x-intercepts.

Then, for (x²-4x+8) = 0, we get:

`b^(2) - 4ac = (-4)^(2)-4(1)(8)=16-32=-16`

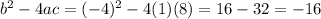
At the same way, for (x²+4x+8) = 0, we get:

`b^(2) - 4ac = (4)^(2)-4(1)(8)=16-32=-16`