Answer:NO
Explanation:
Given
Quadratic equation
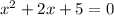
First we need to check discriminant of equation to know whether roots are real of imaginary
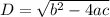
here
a=1, b=2, c=5

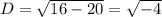
thus D<0 therefore roots are imaginary
To verify given roots are roots of equation
sum of roots
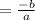
Product of roots

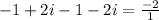
-2=-2
L.H.S=R.H.S
Product of roots
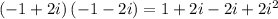
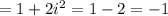
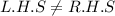
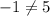
thus given values are not solutions of given equation.