Question

Verify that −1+2i and −1− 2i are solutions to x²+2x+5=0.

Answer 1

Answer:NO

Explanation:

Given

Quadratic equation
`x^2+2x+5=0`

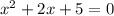
First we need to check discriminant of equation to know whether roots are real of imaginary

`D=√(b^2-4ac)`

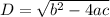
here

a=1, b=2, c=5

`D=√(2^2-4* 1* 5)`

`D=√(16-20)=√(-4)`

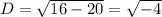
thus D<0 therefore roots are imaginary

To verify given roots are roots of equation

sum of roots
`=(-b)/(a)`

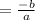
Product of roots
`=(c)/(a)`

`-1+2i-1-2i=(-2)/(1)`

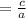
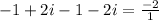
-2=-2

L.H.S=R.H.S

Product of roots

`\left ( -1+2i\right )\left ( -1-2i\right )=1+2i-2i+2i^2`

`=1+2i^2=1-2=-1`

`L.H.S\\eq R.H.S`

`-1\\eq 5`

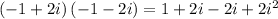
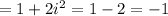
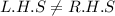
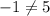
thus given values are not solutions of given equation.