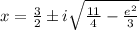Question

Solve the following equations.
log3(x^2 − 3x + 5) = 2

Answer 1

`x=(3)/(2) \pm i\sqrt{(11)/(4)-(e^(2) )/(3)  }`

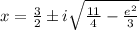
Explanation:

First, cancel logarithms by taking exp of both sides:

`e^{3*(x^(2)-3x+5) }=e^(2) \\ 3*(x^(2)-3x+5)=e^(2)`

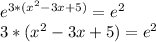
Divide both sides by 3 and then substract 5 from both sides:

`x^(2) -3x=(e^(2) )/(3) -5`

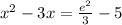
Add 9/4 to both sides in order to write the left side as a square:

`x^(2) -3x+(9)/(4) =(e^(2) )/(3) -(11)/(4)  \\(x-(3)/(2)) ^(2) =(e^(2) )/(3) -(11)/(4)`

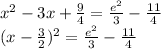
Express the right side as:

`(-1)*((11)/(4)-(e^(2) )/(3) )`

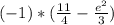
Now take square root of both sides, keep in mind that:
`i=√(-1)`

`x-(3)/(2)=\pm √(-1) *\sqrt{(11)/(4)-(e^(2) )/(3)`

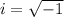
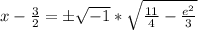
Finally, add 3/2 to both sides:

`x=(3)/(2) \pm i\sqrt{(11)/(4)-(e^(2) )/(3)  }`