Answer:

Explanation:
First, cancel logarithms by taking exp of both sides:
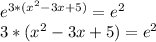
Divide both sides by 3 and then substract 5 from both sides:
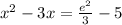
Add 9/4 to both sides in order to write the left side as a square:
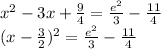
Express the right side as:
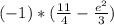
Now take square root of both sides, keep in mind that:
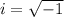
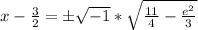
Finally, add 3/2 to both sides:
