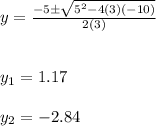Answer:
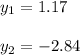
Explanation:
Given the following quadratic equation:
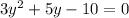
You need to use the Quadratic formula to find the solutions.
The Quadratic formula is:
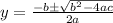
In this case you can identify that:
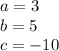
The, substituting this values into the Quadratic formula, you get the following solutions for the given quadratic equation: