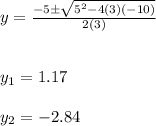Question

3y 2 +5y−10=03, y, squared, plus, 5, y, minus, 10, equals, 0 What are the solutions to the equation above? Choose 1 answer: y=-\dfrac{5}{2}-\dfrac{\sqrt{145}}{2}

Answer 1

`y_1=1.17\\\\y_2=-2.84`

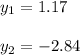
Explanation:

Given the following quadratic equation:

`3y^2 +5y-10=0`

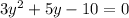
You need to use the Quadratic formula to find the solutions.

The Quadratic formula is:

`y=(-b\±√(b^2-4ac) )/(2a)`

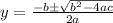
In this case you can identify that:

`a=3\\b=5\\c=-10`

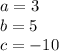
The, substituting this values into the Quadratic formula, you get the following solutions for the given quadratic equation:

`y=(-5\±√(5^2-4(3)(-10)) )/(2(3))\\\\\\y_1=1.17\\\\y_2=-2.84`