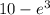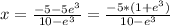Answer:
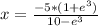
Explanation:
Rewrite the equation, adding 3 to both sides and subtracting log(x-5) from both sides:
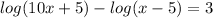
Using the next propierty:
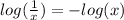
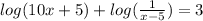
Using this propierty:

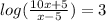
Cancel logarithms by taking exp of both sides:
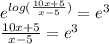
Multiplying both sides by x-5 and factoring:
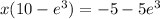
Solving for x multiplying both sides by