Question

Solve the following equations.
log6(x) = 1

Answer 1

x = 6

Explanation:

Given:

log₆(x) = 1

Now,

From the properties of log

logₓ (z)=
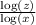`(\log(z))/(\log(x))` (where the base of the log is equal for both numerator and the denominator)

also,

log(xⁿ) = n × log(x)

thus,

using the above properties, we can deduce the results as:

logₓ(y) = n is equivalent to y = xⁿ

therefore,

the given equation can be deduced as:

log₆(x) = 1

into,

x = 6¹

or

x = 6