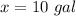Question

Miguel needs 4 gallons of milk to make 12 milkshakes. How much milk does he need to

make 30 milkshakes? Use at least two different methods to support your answer. Is this a
proportional relationship?​

Answer 1

10 gallons of milkshake is needed to make 30 milkshakes.

Yes it is a proportional relationship

Explanation:

We can use proportion to solve this;

Let x be the amount of milk needed to make 30 milkshakes.

4 gallons of milk = 12 milkshakes

x = 30 milkshakes

Cross multiply

12x = 30×4

12x =120

Divide both-side of the equation by 12

12x/12 =120/12

(On the left-hand side of the equation, the 12 at the numerator will cancel-out 12 at the denominator leaving us with just x while on the right-hand side of the equation 120 will be divided by 12)

x=10 gallons

Therefore , 10 gallons of milkshake is needed to make 30 milkshakes

Answer 2

see the procedure

Explanation:

Part 1) using proportion

we know that

Miguel needs 4 gallons of milk to make 12 milkshakes

so

Using proportion

Find out how much milk he needs to make 30 milkshakes

Let

x ----> gallons of milk needed

`(4)/(12)(gal)/(milkshakes)=(x)/(30)(gal)/(milkshakes)\\\\x=30(4)/12\\\\x=10\ gal`

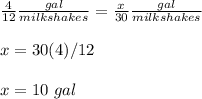
Miguel needs 10 gallons of milk to make 30 milkshakes

Part 2) we know that

A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
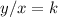`y/x=k` or
`y=kx`

This problem represent a proportional relationship

Let

x ----> the number of gallons of milk

y ----> the number of milkshakes

we know that

Miguel needs 4 gallons of milk to make 12 milkshakes

so

For x=4, y=12

Find out the constant of proportionality k

`k=y/x`

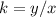
substitute the values

`k=12/4=3\ milkshakes/gallon`

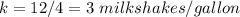
The linear equation is equal to

`y=3x`

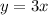
For y=30

substitute in the equation and solve for x

`30=3x`

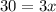
Divide by 3 both sides

`x=10\ gal`