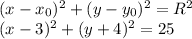Answer:
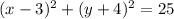
Explanation:
We start by writing the general form of the equation of a circle of radius R centered at
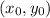 and creating three equations (one for each unknown:
and creating three equations (one for each unknown:
 ,
,
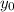 , and the radius R):
, and the radius R):

1) If the circle passes through (0,0) then we should have that the equation above holds true:
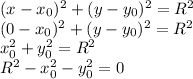
2) If the circle passes through (6,0) then we should have that the equation above holds true, and we also can use the important result from part 1) (
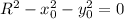 ) to solve for
) to solve for
 :
:
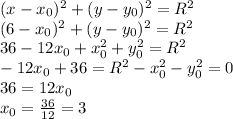
3) If the circle passes through (0,-8) then we should have that the general equation of the circle above holds true, and we also can use the important result from part 1) (
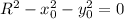 ) to solve for
) to solve for
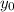 :
:
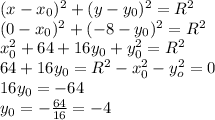
4) and finally, we use the results for
 and
and
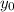 of parts 2) and 3) back into the equation in part 1) to solve for
of parts 2) and 3) back into the equation in part 1) to solve for
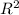 :
:
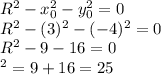
Then, replacing
 ,
,
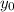 , and
, and
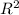 for the values we found, the equation of the circle becomes:
for the values we found, the equation of the circle becomes: