Question

Use the geometric series formulas to find the sum of the geometric series.

1 + √3 + 3 + 3√3 + ⋯ + 243

Answer 1

573.578

Explanation:

Geometric Sequence is the sequence in which every digit is the same multiplier of its previous digit.

The given Sequence is: √3 + 3 + 3√3 + ⋯ + 243

here a₁ = √3, r = 3 ÷ √3 = √3.

First we will find the number of terms for this we use formula:

`a_(n) = a_(1)(r)^(n-1)`

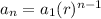
⇒ 243 = √3(√3)ⁿ⁻¹

⇒ (√3)¹⁰ = √3(√3)ⁿ⁻¹

⇒ (√3)⁹ = (√3)ⁿ⁻¹

⇒ n - 1 = 9

⇒ n = 10

The formula of sum of geometric series is:

`S_n=(a_1(1-r^n))/(1-r)`

⇒
`S_n=(√(3)(1-√(3)^(10)))/(1-√(3))`

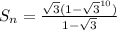
⇒ Sₙ = 572.578147716

Thus the sum of 1 + √3 + 3 + 3√3 + ⋯ + 243 = 1 + 572.578 = 573.578