Question

The Ksp of AgI is 8.3× 10–17. You titrate 25.00 mL of 0.08160 M NaI with 0.05190 M AgNO3. Calculate pAg after the following volumes of AgNO3 are added: (a) at 35.10 mL (b) at Ve (volume at equilibrium) (c) at 47.10 mL

Answer 1

(a) 13.64; (b) 8.04; (c) 2.25

Step-by-step explanation:

AgI(s) ⇌ Ag⁺(aq) + I⁻(aq)

`K_{\text{sp}} = {\text{[Ag$^(+)$][I$^(-)$]} = 8.3* 10^(-17)`

(a) pAg at 35.10 mL

`\text{Moles of I$^(-)$} = \text{0.02500 L} * \frac{\text{0.08160 mol}}{\text{1 L}} = 2.040 * 10^(-3)\text{ mol/L }\\\text{Moles of Ag$^(+)$} = \text{0.03510 L} * \frac{\text{0.05190 mol}}{\text{1 L}} = 1.822 * 10^(-3)\text{ mol/L}`

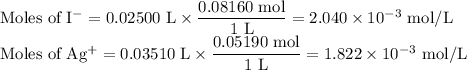
AgI(s) ⇌ Ag⁺(aq) + I⁻(aq)

I/mol: 1.822 × 10⁻³ 2.040 × 10⁻³

C/mol: -1.822 × 10⁻³ -1.822 × 10⁻³

E/mol: 0 0.218 × 10⁻³

We have a saturated solution of AgI containing 0.218 × 10⁻³ mol of excess I⁻.

V = 25.00 mL + 35.10 mL = 60.10 mL

`\text{[I$^(-)$]} = \frac{0.218 * 10^(-3)\text{ mol}}{\text{0.0610 L}} = 3.57 * 10^(-3)\text{ mol/L}\\`

AgI(s) ⇌ Ag⁺(aq) + I⁻(aq)

E/mol·L⁻¹: s 3.57 × 10⁻³ + s

`K_{\text{sp}} = s(3.57 * 10^(-3) + s) = 8.3* 10^(-17)\\`

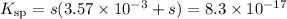
Check for negligibility:

`(3.57 * 10^(-3))/(8.3* 10^(-17)) = 4.3 * 10^(13) > 400\\\\\therefore s \ll 3.63 * 10^(-3)\\K_{\text{sp}} = s* 3.63 * 10^(-3)= 8.3* 10^(-17)\\\\s = \text{[Ag$^(+)$]} = (8.3* 10^(-17))/(3.63 * 10^(-3)) =2.29 * 10^(-14)\\\\\text{pAg} = -\log \left (2.29* 10^(-14) \right) = \mathbf{13.64}`

(b) At equilibrium

AgI(s) ⇌ Ag⁺(aq) + I⁻(aq)

E/mol·L⁻¹: s s

`K_{\text{sp}} = s* s = s^(2) = 8.3* 10^(-17)\\s = \sqrt{8.3* 10^(-17)} = 9.11 * 10^(-9)\\\text{pAg} = -\log \left (9.11 * 10^(-9) \right) = \mathbf{8.04}`

(c) At 47.10 mL

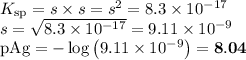
`\text{Moles of Ag$^(+)$} = \text{0.04710 L} * \frac{\text{0.05190 mol}}{\text{1 L}} = 2.444 * 10^(-3)\text{ mol}`

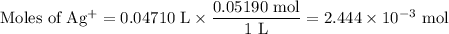
AgI(s) ⇌ Ag⁺(aq) + I⁻(aq)

I/mol: 2.444 × 10⁻³ 2.040 × 10⁻³

C/mol: -2.040 × 10⁻³ -2.040 × 10⁻³

E/mol: 0.404 × 10⁻³ 0

V = 25.00 mL + 47.10 mL = 72.10 mL

`\text{[Ag$^(+)$]} = \frac{0.404 * 10^(-3)\text{ mol}}{\text{0.0721 L}} = 5.61 * 10^(-3)\text{ mol/L}\\\text{pAg} = -\log(5.61 * 10^(-3)) = \mathbf{2.25}`