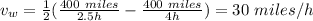Question

An airplane makes a 400-mile trip against a head wind in 4 hours. The return trip takes 2.5 hours, the wind now being a tall wind. If the plane maintains a constant speed with respect to still air, and the speed of the wind is also constant and does not vary, find the still-air speed of the plane and the speed of the wind.

Answer 1

`v_p=130\ miles/h`

`v_w=30\ miles/h`

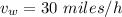
Explanation:

Lets call
`v_p` the the still-air speed of the plane and
`v_w` the speed of the wind. On the first part the speed of the plane relative to the ground will be
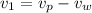`v_1=v_p-v_w`, and on the second part it will be
`v_2=v_p+v_w`.

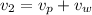We know that the distance d=400 miles on the first and second parts are the same, so by the definition of velocity we will have:

`v_1=(d)/(t1)`

`v_2=(d)/(t2)`

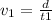
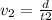
Or:

`v_p-v_w=(d)/(t1)`

`v_p+v_w=(d)/(t2)`

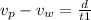
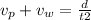
Adding both equations:

`(v_p-v_w)+(v_p+v_w)=2v_p=(d)/(t1)+(d)/(t2)`

`v_p=(1)/(2)((d)/(t1)+(d)/(t2))`

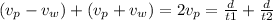
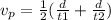
Which for our values is:

`v_p=(1)/(2)((400\ miles)/(4h)+(400\ miles)/(2.5h))=130\ miles/h`

If instead of adding, we substact, we would have:

`(v_p+v_w)-(v_p-v_w)=2v_w=(d)/(t2)-(d)/(t1)`

`v_w=(1)/(2)((d)/(t2)-(d)/(t1))`

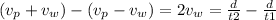
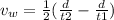
Which for our values is:

`v_w=(1)/(2)((400\ miles)/(2.5h)-(400\ miles)/(4h))=30\ miles/h`