Question

Graph the line given by 2x+y=1 and the circle given by x²+y²=10.Find all solutions to the system of equations. Verify your result both algebraically and graphically.

Answer 1

Algebraically, the point (1, -5) satisfies the first inequality, but it does not satisfy the second inequality because -5 is not greater than -5. Graphically, the point (1, -5) lies in the shaded area of the first inequality but lies on the dashed line of the second inequality, which is not inclusive. Therefore (1, -5) is not a solution to the given system of inequalities.

Answer 2

(1.8, -2.6) and (-1, 3)

Explanation:

`2x+y=1`

`x^2+y^2=10`

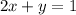
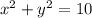
From the first equation

`y=1-2x`

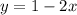
Applying to the second equation

`x^2+(1-2x)^2=10\\\Rightarrow x^2+1+4x^2-4x=10\\\Rightarrow 5x^2-4x-8=0`

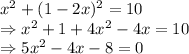
Solving the equation we get

`x=(-\left(-4\right)+√(\left(-4\right)^2-4\cdot \:5\left(-9\right)))/(2\cdot \:5), (-\left(-4\right)-√(\left(-4\right)^2-4\cdot \:5\left(-9\right)))/(2\cdot \:5)\\\Rightarrow x=1.8, -1`

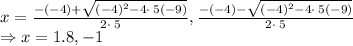
At x = 1.8

Applying in first equation

`2* 1.8+y=1\\\Rightarrow y=1-3.6\\\Rightarrow y=-2.6`

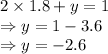
At x = -1

Applying in first equation

`2* -1+y=1\\\Rightarrow y=1+2\\\Rightarrow y=3`

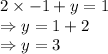
∴ The circle and line intersect at points (1.8, -2.6) and (-1, 3)