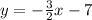Answer:
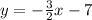
Explanation:
Line L has the equation:
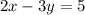
we need to clear for y:
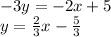
now we have the form a general line equation

where
 is the slope of the line.
is the slope of the line.
so the slope of the line L is:
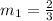
and for two lines to be parallel the following condition must be met
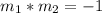
where
 in this case is the slope of line M, substituting the value
in this case is the slope of line M, substituting the value
 to find
to find
 :
:
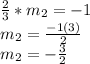
This is the slope of line M, and since we also know that it passes through the point (2, -10) where
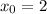 and
and

we use the point- slope equation and substitute known values to find the equation of the line M:
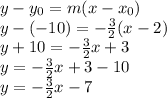
the equation of line M is: