Answer:
⇒ ( log(3) + log(4) ) + log(5) − log(6)
or
⇒ log(3 × 4) + log(5) - log(6)
or
⇒ log(12) + log(5) - log(6)
or
⇒ log(12 × 5) - log(6)
or
⇒ log(60) - log(6)
or
⇒

or
⇒ log(10)
also,
log(10) = 1
Explanation:
Given equation;
log(3) + log(4) + log(5) − log(6) = 1
now, we know the property of log function as:
1) log(A) + log(B) = log(AB)
and,
2) log(A) - log(B) =
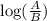
therefore, applying the property (1) on the LHS
⇒ ( log(3) + log(4) ) + log(5) − log(6)
or
⇒ log(3 × 4) + log(5) - log(6)
or
⇒ log(12) + log(5) - log(6)
again applying the property (1)
⇒ log(12 × 5) - log(6)
or
⇒ log(60) - log(6)
now applying the property 2, we get
⇒

or
⇒ log(10)
also,
log(10) = 1
Hence,
LHS = 1 = RHS
Hence, proved