Question

Use properties of logarithms to show that log(3) + log(4) + log(5) − log(6) = 1

Answer 1

⇒ ( log(3) + log(4) ) + log(5) − log(6)

or

⇒ log(3 × 4) + log(5) - log(6)

or

⇒ log(12) + log(5) - log(6)

or

⇒ log(12 × 5) - log(6)

or

⇒ log(60) - log(6)

or

⇒
`\log((60)/(6))`

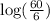
or

⇒ log(10)

also,

log(10) = 1

Explanation:

Given equation;

log(3) + log(4) + log(5) − log(6) = 1

now, we know the property of log function as:

1) log(A) + log(B) = log(AB)

and,

2) log(A) - log(B) =
`\log((A)/(B))`

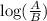
therefore, applying the property (1) on the LHS

⇒ ( log(3) + log(4) ) + log(5) − log(6)

or

⇒ log(3 × 4) + log(5) - log(6)

or

⇒ log(12) + log(5) - log(6)

again applying the property (1)

⇒ log(12 × 5) - log(6)

or

⇒ log(60) - log(6)

now applying the property 2, we get

⇒
`\log((60)/(6))`

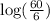
or

⇒ log(10)

also,

log(10) = 1

Hence,

LHS = 1 = RHS

Hence, proved